|
更新の際に構造を変える事があります。 構造を変えるとアドレスが一から再配分されますので
ブックマーク等でお気に入りのページに飛んだ際に、目的と違うページが表示されることがあります。
その場合は画面一番下の [ TOP ] からトップページへ移動して、トップページから
目的のページへ移動してください。 お手数ですがよろしくお願いいたします。
クルマ雑学
| 左右輪間で荷重移動しても両輪の生む摩擦力は同じでは?
|
|
【問】アモントンの摩擦法則は、
[摩擦力]=[摩擦係数]×[荷重]
です。
したがって、
[前輪もしくは後輪いずれかの摩擦力]
=[左タイヤの荷重]×[摩擦係数]+[右タイヤの荷重]×[摩擦係数]
となります。
式の右側を纏めると
[前輪もしくは後輪いずれかの摩擦力]=([左タイヤの荷重]+[右タイヤの荷重])×[摩擦係数]
となります。
左右方向への荷重移動がなければ、
[左タイヤの荷重]=[右タイヤの荷重]=[軸重]×50%
ですから、上式は
[前輪もしくは後輪いずれかの摩擦力]=([軸重]×50%+[軸重]×50%)×[摩擦係数]
となり、
[前輪もしくは後輪いずれかの摩擦力]=[軸重]×[摩擦係数]
と置き換えることが出来ます。
さて、左右方向への荷重移動が生じて
■[左タイヤの荷重]=[軸重]×70%
■[右タイヤの荷重]=[軸重]×30%
になったと仮定します。
この時上式は
[前輪もしくは後輪いずれかの摩擦力]=([軸重]×70%+[軸重]×30%)×[摩擦係数]
となり、やはり
[前輪もしくは後輪いずれかの摩擦力]=[軸重]×[摩擦係数]
と置き換えることが出来ます。
であれば、左右方向へ荷重移動しても、前輪なり後輪なりの摩擦力は変わらないことになります。
ということは、重心が高くてもアライメント変化さえ抑えれば、重心の低いクルマと同じ旋回性能が発
揮されるのではありませんか?
□□□□□■■■■■□□□□□■■■■■□□□□□■■■■■□□□□□
【答】(すいませんが、スキャナの調子が悪いのでグラフ図はプリントスクリーン→トリミング→JPEG変換しました。 少々見辛
いと思いますが、いずれスキャナの画像と差し替えますので、今しばらく御辛抱下さい)
重い物と軽い物の落下加速度が同じであるためには、空気抵抗を無視しなければなりません。
同様に物理法則の幾つかは、非現実的な前提条件に於いてのみ成立します。
アモントンの摩擦式も、タイヤやブレーキパッドの摩擦に於いて数式通りに成立することが出来ませ
ん。
アモントンの摩擦法則をグラフ化すると下図の二重線を描きます。
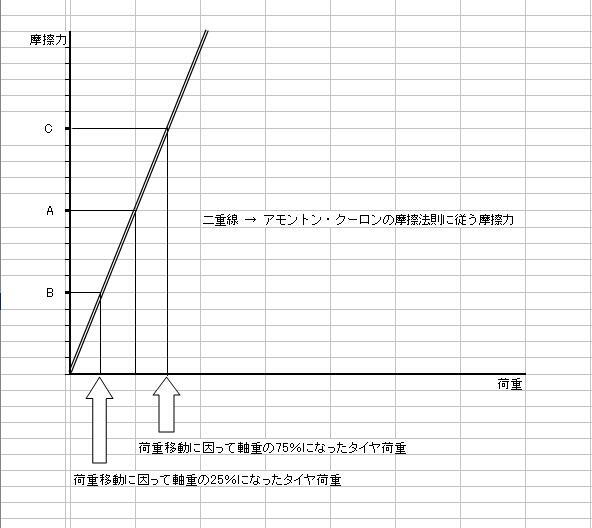
この図に於いてx軸に軸重の50%とると、y軸の目盛り(A点)は10です。
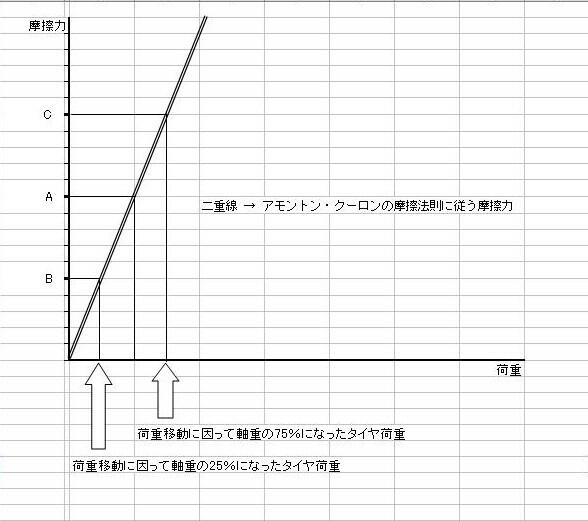
x軸が25%になれば、y軸の目盛り(B点)は5、x軸が75%になれば、y軸の目盛り(C点)は15。
つまり、
B+C=A×2
が成立しています。
タイヤやブレーキパッドなど現実に作用する摩擦力の多くは「飽和的摩擦力」と呼ばれます。
この摩擦力は、アモントンの摩擦法則と同様に、荷重の増大に伴って増大するのですが、荷重があ
る程度の大きさを超えると、摩擦力の増大が頭打ちになります。
これをグラフ化すると下図の点線のようになります。
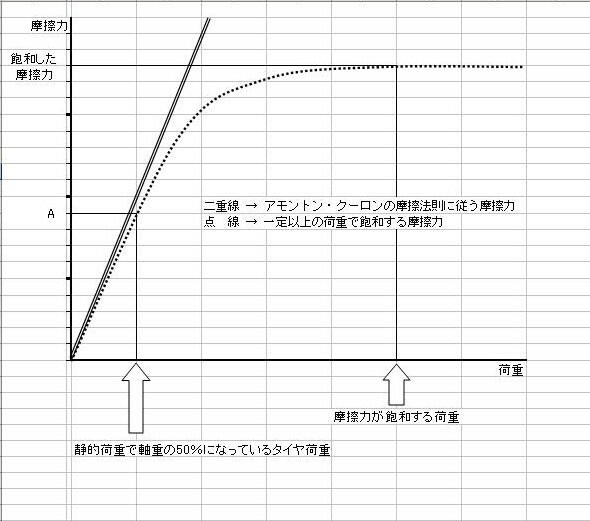
荷重が大きくなるにつれて、実際の摩擦力がアモントンの摩擦式と乖離していくのが分かります。
この図に於いてx軸に軸重の50%とると、y軸の目盛り(A点)は9です。
9×2=18
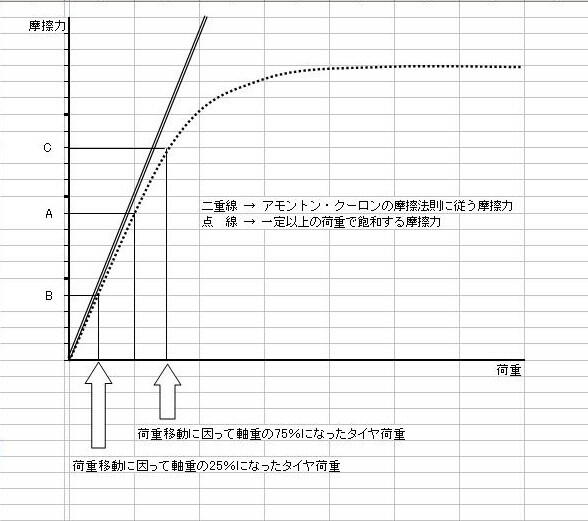
x軸が25%になれば、y軸の目盛り(B点)は4、x軸が75%になれば、y軸の目盛り(C点)は13。
4+13=17
つまり、
B+C<A×2
となるのです。
これは、実車に於ける荷重と摩擦力の関係は、荷重移動が大きくなるほど摩擦力の総和が小さくな
ることを示しています。
だから、トレッドやホイールベースの長さに比して重心の高いクルマ(=荷重移動量の多くなり易いク
ルマ)は、求心加速度が小さくなってしまうのです。
|
|
|
|