|
�X�V�̍ۂɍ\����ς��鎖������܂��B�@�\����ς���ƃA�h���X���ꂩ��Ĕz������܂��̂�
�u�b�N�}�[�N���ł��C�ɓ���̃y�[�W�ɔ�ۂɁA�ړI�ƈႤ�y�[�W���\������邱�Ƃ�����܂��B
���̏ꍇ�͉�ʈ�ԉ��� [ TOP ] ����g�b�v�y�[�W�ֈړ����āA�g�b�v�y�[�W����
�ړI�̃y�[�W�ֈړ����Ă��������B�@���萔�ł�����낵�����肢�������܂��B
�^�C��
|
|
�y��z�u�R���p�E���h�������Ȃ�A�^�C���̕�������Ă��O���b�v�͓͂����v���ƕ����܂����B
�@���������Ȃ�A�n�C�h���v���[�j���O���ۂ̊댯����`���Ă܂ō����\�Ԃɑ����^�C���𗚂������
�͉��̂Ȃ̂ł��傤�H
����������������������������������������������������������������������
�y���z�u�^�C���̕�������Ă��O���b�v�͓͂����v���Ƃ��Ă��A�����b�g�͂���܂��B�@�@�P�ʖʐς�����̕�
�ׂ����Ȃ��Ȃ�̂Ń^����Ȃ�܂��B
�@�ł��A����ȑO�̖��ŁA�u�R���p�E���h�������ł��A�^�C���̕����������O���b�v�͈͂قȂ�v����
���ł���B
�@���Z�̗��T�Ŋw�ԁw�A�����g���̖��C�@���x�ɋ���A[ ���C�� ] �� [ ���C�W�� ] �~ [ �d ] �ł��B
�@�@�������ĕ�����ʂ�A���̖@���ɏ]�����薀�C�͖͂��C�ʐςɈˑ����܂���i�������́g�����|����
���C�ʐςɈˑ����Ȃ��h�j�B
�@�ł����A�N���}�̃^�C���͂��̖@���ɏ]���܂���B
�@���̖@���ɏ]������A���C�͉͂d�̑傫���ɑ��Ė����ɔ�Ⴕ�܂��B
�@�Ƃ��낪�A�^�C���͉d�����傷��ɂ�Ė��C�W���������čs���A�₪�Ė��C�͂��O�a���܂��i��
��ȍ~���d������������ƁA���C�͂��ɂ₩�ɒቺ���n�߂�j�B
�@�����Ȃ݂ɁA���́y�N���}�G�w�z�̍��ɂ���w���E�֊Ԃʼnd�ړ����Ă����ւ̐��ޖ��C�͓͂����ł́H�x�ɏ������}���Q
�l�ɂȂ�Ǝv���܂��B
�@�ł�����A
[ �y�d�̍������C�W�� ] �~ [ �����^�C���̍L���ڒn�ʐ� ] �� [ �d�d�̒Ⴂ���C�W�� ]
�~ [ �ׂ��^�C���̋����ڒn�ʐ� ]
�@�ɂȂ�킯�ł��B
�@�������A���ӂ��ė~�����̂� [ �^�C���̕��̍� ] �� [ �ڒn�ʐς̍� ] �ł͂Ȃ��Ƃ������Ƃł��B
�@�^�C���̐ڒn�ʂ́A���ł���^�C�����ԏd�Œׂ���ĕ���ɂȂ邱�Ƃɂ���ďo���Ă��܂��B
�@�ł�����A�^�C���̕����L���Ȃ�Γ��ł���^�C���̍����������Ȃ�A�ԏd�Œׂ����Ȃ�܂��B
�@����䂦�ɁA [ �^�C���̕��̍� ] �� [ �ڒn�ʐς̍� ] �ɂȂ�܂��B
�@�u�႟�T�A�^�C���̕����Ⴄ�ƃO���b�v�͂ɍ����o����[�Ă��A���܂�債��������Ȃ����
�[�́v���ăc�b�R�~�����肻���ł����A���̓^�C���̕���������ۂɃO���b�v�͂ɍ��������闝�R�́A��
�ɂ������ł��B
�@���̗����͏c�����̃O���b�v�͂ɂ͗]��e�����Ȃ��̂ł����A�������̃O���b�v�͂ɂ͌��\�e����
�܂��B
�@�^�C���̐ڒn�ʂ́A���ł���^�C�����ԏd�Œׂ���ĕ���ɂȂ邱�Ƃɂ���ďo���Ă���̂ł�����A
�^�C���̍\���̂͗]��ɂ����������Ɛڒn�ʐς������Ȃ��Ă��܂��܂��B
�@�����Ŋ�炩�͝���A�ڒn�ʐς��҂����x�̍����ɗ��߂Ă���̂ł����A���̍����̒Ⴓ�A����сA
��C���ŃT�C�h���Č`�̂�ۂ��Ă���Ƃ�����C����^�C���̍\���䂦�ɁA���͂���Ƃ��ɂ��^
�C���͝���܂��B
�@�����̂悤�ɁA���͂���ۂɃ^�C�����c�ނ̂ł��B
�@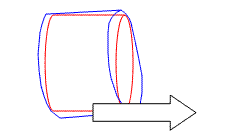
�@�Ԃ������A���~�z�C�[���A�������^�C���̊O���A����́i���Ȃ狁�S�́j�ł��B
�@���̝���i�c�݁j�Ɉ����āA�^�C���̐ڒn�ʂ��̂��̂̏ꏊ�ɉ�����ڒn������܂��B
�@��}�ł����Ȃ�A�����͐ڒn�����オ���āA�E���͐ڒn����������̂ł��B
�@���́y�N���}�G�w�z�̍��ɂ���w���E�֊Ԃʼnd�ړ����Ă����ւ̐��ޖ��C�͓͂����ł́H�x�Ő���
�����Ē������ʂ�A�d����Ɩ��C�͂̑��a�͏������Ȃ�܂��B�@�@�܂�A���͂Ɉ����ă^�C������
��i�c�ށj�ƃO���b�v�͂��ቺ����� �^�C�����ƃO���b�v�͂̊W�ł��B
�@�^�C���̍\���Ɏg���Ă���p�[�c�������ł����Ă��A�����L���Ȃ�Γ������͂������Ă��^�C
���̝���i�c�݁j�͏��Ȃ��Ȃ�܂��B�@�@�܂�A����i�c�݁j��Ȃ邪�䂦�ɁA���̍L���^�C���͍�����
�͂������郏�P�ł��B
�@�ł�����A�����T�C�Y�̃^�C���ł��\�����������ɂ���A��荂�����͂������邱�ƂɂȂ�܂�
�i���������x���B�@�@�ڒn�ʐς��̂��̂��啝�ɋ����Ȃ��Ă��܂��悤�ł͋t���ʁj�B
�@�����������R������A�����T�C�Y�̃^�C���ł��n�C�O���b�v�u���̃^�C���̕����R���t�H�[�g�u���̃^�C
���������S�n�������̂ł��B
�@�����̗��R�ɂ��A�R���p�E���h��\���������ł��A�^�C���̕����������O���b�v�͈͂قȂ�̂�
���B
�@�܂��A�����łȂ�������n�C�p���[�Ԃɂ킴�킴�n�C�h���v���[�j���O���ۂ̊댯����`���Ă܂ő���
�^�C���𗚂����͂��܂���B�@�@��C��R�����đ������ł�����ˁB
|
|
|
|